数据结构

基本定义

程序 = 数据结构 + 算法
算法 = 指令的有限序列

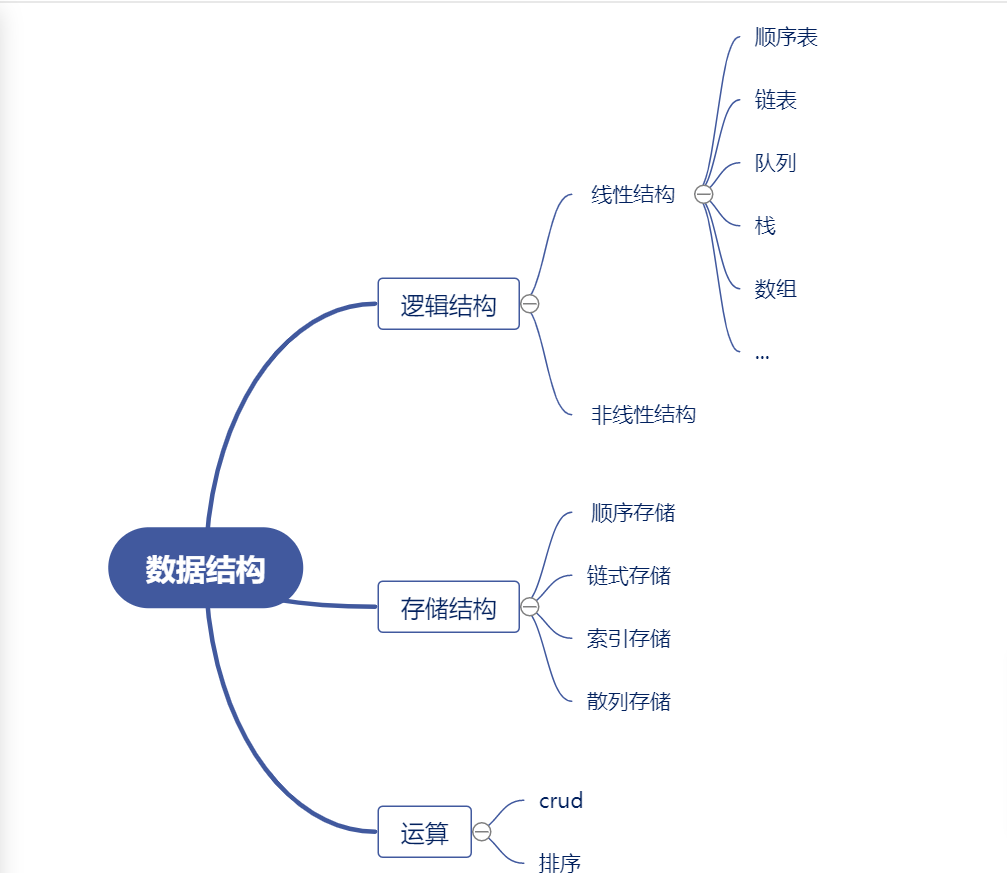
数据结构 = 结构 + 运算

结构 = 逻辑结构 + 存储结构
运算 = 增删改查 排序

https://www.apowersoft.cn/faq/how-to-use-mind-map.html?apptype=aps-bd&appver=1.0.3.0&ct=1610360794&h=63818322d10a55b1d335b44ea4789f59&language=zh&mt=1610360825&product_id=313&type=install&wxga=#_1-1-chapter

xmind使用说明文档

---

复杂度

时间频度函数

基本语句执行的频数

基本语句:执行次数最多的语句

T(n) = 2n^2 + n + 7
T(n) = n^2 + 2n + 1
...

关于参数 n 的时间频度函数，从 T(n)得出 O(n)

O(最坏情况)
欧米伽(最好情况) w
西塔(平均)

时间复杂度

核心代码的执行次数量级 计算：得出时间频度函数，只保留最高阶的项

T(n) = An^2 + Bn + Cn^0
O(n) = n^2

//	O(n)
count = 0;
for(int i = 0; i<n; i++){
    count ++;
}


//	O(n^2)
count = 0;
for(int i = 0; i<n; i++){
    for(int j = 0; j<n; j++){
    	count ++;
		}
}

//	O(log2 n)
for(int i = 1; i<=n; i=i*2){
    count ++;
}

//	外层 n 次
//	内层总共 0 + 1 + 2 + ... + n = (1+n)n/2 , 平均(1+n)/2次
//	T(n) = n*(1+n)/2 = 1/2n^2 + 1/2 n
//	O(n^2)
for(int i = 0; i<n; i++){
    for(int j = 0; j<i; j++){
        count ++;
    }
}

空间复杂度

在内存中，变量的占用量化--> 变量的个数

---

线性表

线性表的基本操作

package mawenshu.liner;

public interface List {
    int size();

    boolean isEmpty();

    void add(int index, Object object);

    void add(Object object);

    Object removeByIndex(int index);

    Object remove(Object object);

    Object replaceByIndex(int i, Object object);

    Object replace(Object oldObject, Object newObject);

    Object get(int i);
}

线性表之顺序表

基本概念与图示

使用地址连续的存储单元存储数据

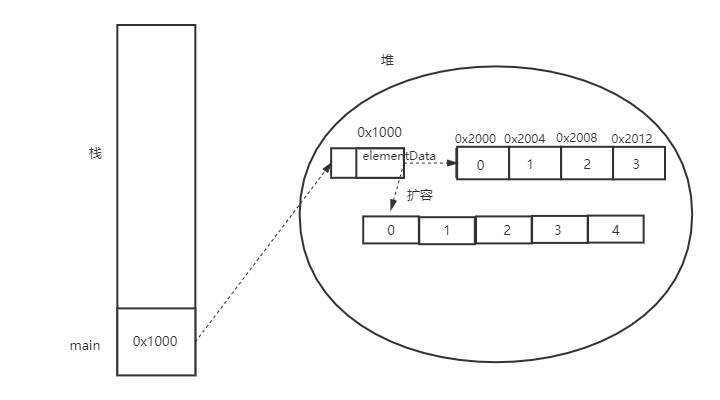
顺序表实现

import mawenshu.liner.List;
import mawenshu.liner.MyArrayIndexOutOfBoundsException;
/**
 * @author 马文澍
 * @date 2021/1/12 15:33
 */
public class ArrayList implements List {
    private int size;   //  元素的个数
    private Object[] elementData;   //  采用数组实现可扩容顺序表

    public ArrayList() {
        this(4);
    }

    public ArrayList(int initCapacity) {
        elementData = new Object[initCapacity];
    }

    @Override
    public int size() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        return this.size == 0;
    }

    @Override
    public void add(int index, Object object) {
        //  判断是否满了，需要扩容
        if (isFull()) {
            grow();
        }
        //index后面的每个元素后移一位，从最后一个开始移动
        for (int i = size; i > index; i--) {
            this.elementData[i] = this.elementData[i - 1];
        }
        this.elementData[index] = object;
        this.size += 1;    //  元素个数加一
    }


    @Override
    public void add(Object object) {
        this.add(this.size, object);
    }


    @Override
    public Object removeByIndex(int index) {
        //  index后面的元素前移一位,从index开始
        Object object = this.elementData[index];
        for (int i = index; i < this.size - 1; i++) {
            this.elementData[i] = this.elementData[i + 1];
        }
        this.elementData[size - 1] = null;
        this.size--;
        return object;
    }

    @Override
    public Object remove(Object object) {
        for (int i = 0; i < this.size; i++) {
            if (this.elementData[i].equals(object)) {
                removeByIndex(i);
                i--;//后面一位新的元素前移到了刚刚比较的那个位置, 遍历应该应当回退到刚刚比较的那个位置
            }
        }
        return object;
    }

    @Override
    public Object replaceByIndex(int i, Object object) {
        if (IllegalIndex(i)) {
            thr/ow new MyArrayIndexOutOfBoundsException("数组下标越界:" + i);
        }
        return this.elementData[i] = object;
    }

    @Override
    public Object replace(Object oldObject, Object newObject) {
        for (int i = 0; i < this.size; i++) {
            if (this.elementData[i].equals(oldObject)) {
                this.replaceByIndex(i, newObject);
            }
        }
        return newObject;
    }

    @Override
    public Object get(int i) {
        if (IllegalIndex(i)) {
            thr/ow new MyArrayIndexOutOfBoundsException("数组越界异常" + i);
        }
        return this.elementData[i];
    }

    private boolean isFull() {
        return this.size == this.elementData.length;
    }

    /**
     * 扩容后的临时数组 newObject
     * 扩容策略，增加原来容量的一半
     * Object[] newObject = new Object[newLength];
     * for (int i = 0; i < this.size; i++) {
     * newObject[i] = this.elementData[i];
     * }
     * this.elementData = newObject;
     * 右移一位: this.elementData.length >> 1
     */
    private void grow() {
        int newLength = this.elementData.length + (this.elementData.length >> 1);
        this.elementData = Arrays.copyOf(this.elementData, newLength);
    }

    private boolean IllegalIndex(int index) {
        return index >= this.size;
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder("[");
        for (int i = 0; i < size; i++) {
            if (i == size - 1) {
                stringBuilder.append(this.elementData[i]);
            } else {
                stringBuilder.append(this.elementData[i]).append(" ,");
            }
        }
        stringBuilder.append("]");
        return stringBuilder.toString();
    }
}

---

线性表之链表

基本概念与图示

存储单元地址不连续的各个结点一对一单向或者双向链接

添加结点

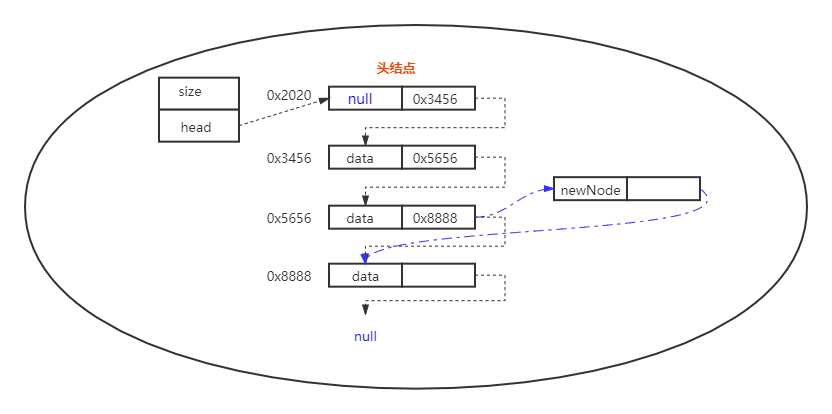
删除结点

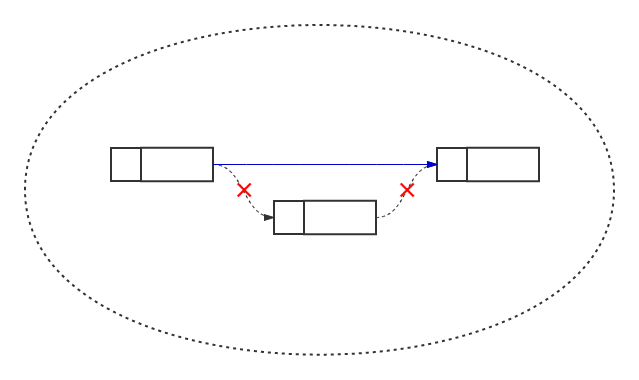
结点类

/**
 * @author 马文澍
 * @date 2021/1/13 16:42
 */
public class Node {
    //  数据域
    Object data;
    //  指针域:    下一个元素
    Node next;
}

链表实现类

package mawenshu.liner.linkedlist;

import mawenshu.liner.List;

/**
 * @author 马文澍
 * @date 2021/1/13 16:43
 */
public class SingleLinkedList implements List {
    private int size;
    private Node head;

    public SingleLinkedList() {
        this.head = new Node();
        this.head.data = null;
        this.head.next = null;
        this.size = 0;
    }

    @Override
    public int size() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        return this.size == 0;
    }

    @Override
    public void add(int index, Object object) {
        //  临时结点，初始指向头结点
        Node p = head;	//	即p和head指向同一个地址，这个地址是一个数据域为空，指针域初始值也为null

        //  遍历链表，查询到要插入的节点的上一个结点
        for (int i = 0; i < index; i++) {
            p = p.next;
        }

        Node newNode = new Node();
        newNode.data = object;

        newNode.next = p.next;
        p.next = newNode;

        size += 1;
    }

    @Override
    public void add(Object object) {
        this.add(size, object);
    }

    @Override
    public Object removeByIndex(int index) {
        Node p = head;
        //  找到要删除的结点的前一个结点
        for (int i = 0; i < index; i++) {
            p = p.next;
        }

        Node currentPoint = p.next;
        //  前一个结点的后继指针置为当前指针的后一个
        p.next = currentPoint.next;
        //  当前指针所指向的数据被丢弃，不指向任何结点，等待GC
        currentPoint.next = null;
        size--;
        return currentPoint.data;
    }

    @Override
    public Object remove(Object object) {
        Node p = head;
        for (int i = 0; i < size; i++) {
            if (p.next.data.equals(object)) {
                removeByIndex(i);
                //  链表数据自动前移，下标不变，size-1
                i--;
            } else {
                //  开始移动指针
                p = p.next;
            }
        }
        return object;
    }

    @Override
    public Object replaceByIndex(int i, Object object) {
        //  指向头结点(空)
        Node p = head;
        for (int j = 0; j <= i; j++) {
            p = p.next;
        }
        p.data = object;

        return object;
    }

    @Override
    public Object replace(Object oldObject, Object newObject) {

        Node p = head;
        for (int i = 0; i < size; i++) {
            p = p.next;
            if (p.data.equals(oldObject)) {
                replaceByIndex(i, newObject);
            }
        }
        return newObject;
    }

    @Override
    public Object get(int i) {
        Node p = head;
        for (int j = 0; j <= i; j++) {
            p = p.next;
        }
        return p.data;
    }

    @Override
    public String toString() {
        Node p = head.next;
        StringBuilder stringBuilder = new StringBuilder("[");
        for (int i = 0; i < size; i++) {
            if (i == size - 1) {
                stringBuilder.append(p.data);
            } else {
                stringBuilder.append(p.data).append(" ,");
            }
            p = p.next;
        }
        stringBuilder.append("]");
        return stringBuilder.toString();
    }
}

特殊的线性表之栈

基本概念

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

总的来说，栈也是一个线性存储结构，不过它受到了一定的限制，先进后出、后进先出（ FILO,LIFO）

栈的数据结构

对栈有基本的三种操作：进栈 push、出栈 pop、查看 peek

public interface Stack{
    boolean push();
    Object pop();
    Object peek();
}🤪

队列 ❀

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

队列的数据元素又称为队列元素。在队列（队尾）中插入一个队列元素称为入队，从队列（队头）中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。

队列的种类

1、双端队列: 不局限于从rear进从front出，两端均可以出入
2、输入受限队列:出队列两边都可以，入队列只能从队尾进rear+1；
3、输出受限队列:入队列两边都可以，出队列只能从队首进front+1；

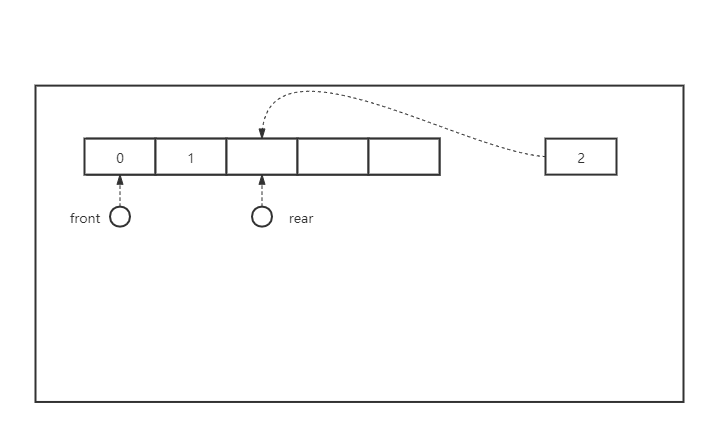
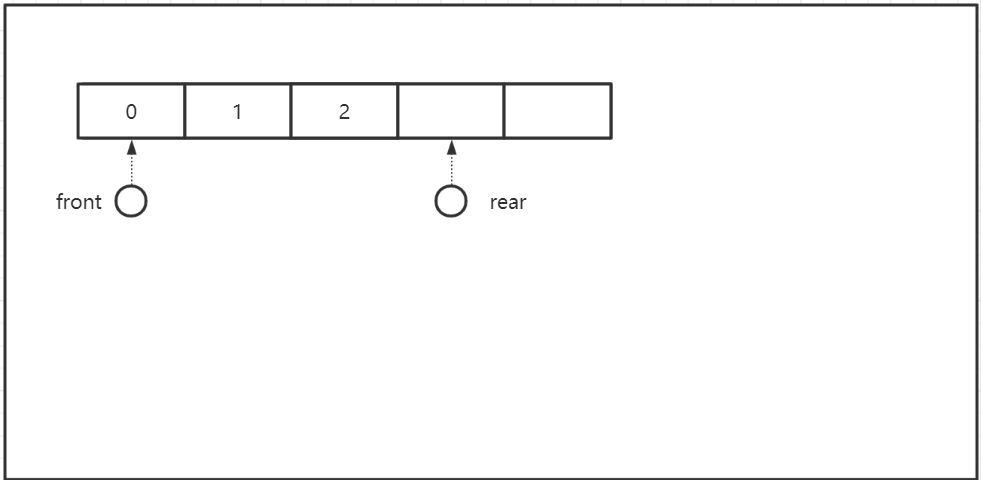
顺序队列

一排队列，队列中元素用过了的资源不可以循环使用，造成了空间浪费

实现

// 数据结构
stack Queue{
  int front = 0; //队头指针
  int rear = 0; //队尾指针
  ElementData elements[MAX_SIZE];
}

初始状态 队空： Q.rear = Q.front = 0;
添加一个数据: 队尾指针上移， Q.rear ++;
弹出一个数据: 队头指针上移， Q.front ++;

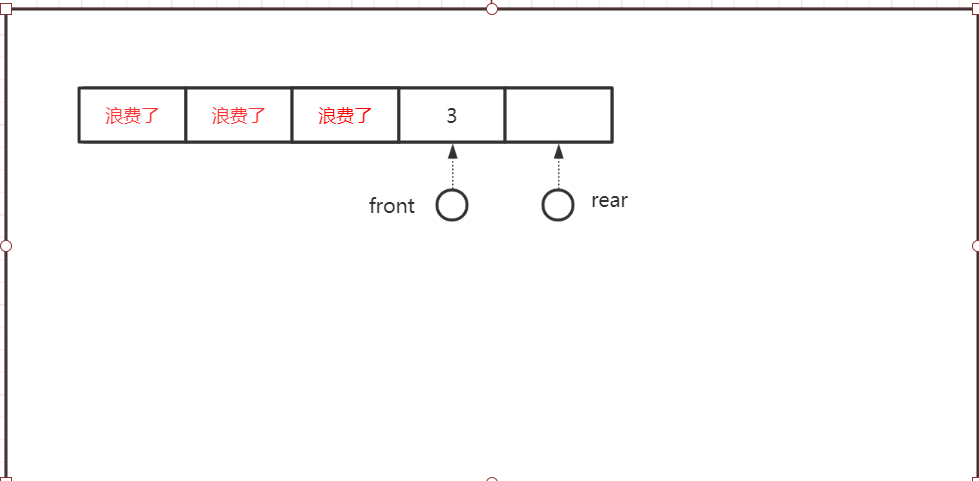
当Q.rear = MAX_SIZE 时无法再加入数据， 队满，
但是实际上， 队列完全可能此时有剩余空间(有的元素可能弹出去了)

这就造成了空间的浪费

使用循环队列解决对于空间的浪费

循环队列

队尾没有地方可以在插入新的元素时，就让新来的元素放在队首没有被元素占据的空位处

顺序方式实现队列

当 rear=size,  front != 0 时， 让rear重新指向开始的索引 0，
即做取余运算, 复用空间， 让数组模拟出一个环形:  即 当还有空间时， 重新利用空间

1⃣️ 初始状态(队空): Q.rear = Q.front = 0;

2⃣️ 入队列(入满):  Q.rear = MAX_SIZE - 1, 索引从 0 到 MAX_SIZE-1
此时: Q.front = 0

3⃣️ 出队列(队头出一个)：Q.front += 1,
元素个数:  Q.rear - Q.front

传统的判断条件队满已经不满足
可以腾出一个空间， 不让Q.rear 指向 Q.front避免和 队空条件冲突，
即队满条件是: Q.rear 尾随 Q.front 后  ：  Q.rear + 1 =  Q.front

对上述相关状态进行取余操作
队空:  Q.rear = Q.front
入队:  Q.rear =  (Q.rear + 1 ) %MAX_SIZE
出队:  Q.front = (Q.front + 1)%MAX_SIZE
队满: （Q.rear + 1） % MAX_SIZE =  Q.front
元素个数:  (Q.rear - Q.front + MAX_SIZE)  % MAX_SIZE

树

二叉树

就是像倒着的树一样，每个分支只会分成最多两个子分支

**根结点：**F

树叶：A、B、H、M

**树的高度(深度)：**有几层？4

常用结论

第 i 层	做多有 n 个结点
1	1
2	2
3	4
4	8
...	...
i	n = 2^(i-1)
合计	$2^i-1$

满二叉树

每一层的结点数目都是 2^(i-1)个(n>=1)

完全二叉树

最下面一层的结点数目小于等于满二叉树的结点数目，并且，去掉的那些结点是从右往左挨个取

---

二叉树的存储

1、顺序存储

从上到下，从左到右存入数组中

如图二叉树:
								  1
							  /   \
							4		    2
							  \   /   \
							   5 3		 6
							   			     \
							   				    7
假设1存储在数组中的下标为0 -------------------> i
则1的左孩子存储在数组中的下标为2*0+1 ----------->2*i+1
则1的右孩子存储在数组中的下标为2*0+2 ------------>2*i+2

反过来，若左孩子下标为k, 右孩子为k+1
则父亲为 (k-1) /2

如下表示上述的树
下表:[0][1][2][3][4][5][6][7][8][9][10][11][12][13][14]
数据:[1][4][2][ ][5][3][6][ ][ ][ ][  ][  ][  ][  ][ 7]
可见，要找到7号的父结点，只需要将 7的元素的下标14 -1 整除2,得到父亲节点的下标

2、链式存储

上述顺序存储有时候会浪费大量的存储空间

结点类有三个域，其中两个指针域分别指向他的左孩子和右孩子

class Node{
    Object data;
    Node left;
    Node right;
}

3、遍历二叉树(链式存储)

核心就是对左子树leftChild，右子树rightChild，根结点root的排列组合

leftChild、rightChild、root有6中不同的排列
约束条件:必须先遍历左子树，再遍历右子树
则有三种不同的排列，分别为：

(三种均为递归遍历)
root leftChild rightChild ----->先序(根)遍历
leftChild root rightChild ----->中序(根)遍历
leftChild rightChild root ----->后序(根)遍历

如图二叉树:
								  1
							  /   \
							4		    2
							  \   /   \
							   5 3		 6
							   			     \
							   			      7
先序遍历
1 4 5 2 3 6 7
中序遍历
4 5 1 3 2 6 7
后序遍历
5 4 3 7 6 2 1
二叉树的高度
4
二叉树的结点数目
7
层序遍历
1
4 2
5 3 6
7
非递归中序遍历
4 5 1 3 2 6 7

基于链表的实现

结点类

public class Node {
    Object data;
    Node leftChild;
    Node rightChild;

    public Node() {
    }

    public Node(Object data, Node leftChild, Node rightChild) {
        this.data = data;
        this.leftChild = leftChild;
        this.rightChild = rightChild;
    }
}

二叉树接口

package mawenshu.btree;

public interface BinaryTree {

    boolean isEmpty();

    //	结点的个数
    int getSize();

    //	树的深度(有几层)
    int getHeight();

    //  先序遍历
    void preOrderTraverse();

    //  中序遍历
    void inOrderTraverse();

    //  后序遍历
    void postOrderTraverse();
}

基于链表的实现类

package mawenshu.btree.linkdetree;


import mawenshu.btree.BinaryTree;

/**
 * @author 马文澍
 * @date 2021/1/15 12:38
 */
public class LinkedBinaryTree implements BinaryTree {
    private Node root;

    public LinkedBinaryTree() {
    }

    public LinkedBinaryTree(Node root) {
        this.root = root;
    }

    @Override
    public boolean isEmpty() {
        return this.root == null;
    }

    /**
     * 二叉树的结点数量
     *
     * @return 0
     */
    @Override
    public int getSize() {
        System.out.println("二叉树的结点数目");
        return getSize(this.root);
    }

    private int getSize(Node node) {
        if (node == null) {
            return 0;
        } else {
            int leftTreeSize = getSize(node.leftChild);
            int rightTreeSize = getSize(node.rightChild);

            return leftTreeSize + rightTreeSize + 1;
        }
    }

    @Override
    public int getHeight() {
        //  二叉树的高度
        System.out.println("二叉树的高度");
        return getHeight(this.root);
    }

    private int getHeight(Node node) {
        if (node == null) {
            return 0;
        } else {
            //  左子树的高度
            int leftTreeHeight = getHeight(node.leftChild);
            //  右子树的高度
            int rightTreeHeight = getHeight(node.rightChild);

            //  取高度较高的一个加一:父结点高度占一个
            return leftTreeHeight > rightTreeHeight ? leftTreeHeight + 1 : rightTreeHeight + 1;
        }
    }

    @Override
    public void preOrderTraverse() {
        if (this.root != null) {
            //  输出根
            System.out.print(this.root.data + " ");
            //  左子树递归遍历
            new LinkedBinaryTree(this.root.leftChild).preOrderTraverse();

            //  右子树递归遍历
            new LinkedBinaryTree(this.root.rightChild).preOrderTraverse();
        }
    }

    @Override
    public void inOrderTraverse() {
        System.out.println("中序遍历");
        inOrderTraverse(this.root);
        System.out.println();
    }

    private void inOrderTraverse(Node node) {
        if (node != null) {
            //  遍历左子树
            inOrderTraverse(node.leftChild);

            System.out.print(node.data + " ");

            //  遍历右子树
            inOrderTraverse(node.rightChild);
        }
    }

    @Override
    public void postOrderTraverse() {
        System.out.println("后序遍历");
        postOrderTraverse(this.root);
        System.out.println();
    }

    private void postOrderTraverse(Node node) {
        if (node != null) {
            postOrderTraverse(node.leftChild);

            postOrderTraverse(node.rightChild);

            System.out.print(node.data + " ");
        }
    }
}

构造二叉树

Node node7 = new Node(7, null, null);
Node node6 = new Node(6, null, node7);
Node node3 = new Node(3, null, null);
Node node5 = new Node(5, null, null);
Node node2 = new Node(2, node3, node6);
Node node4 = new Node(4, null, node5);
Node node1 = new Node(1, node4, node2);

LinkedBinaryTree tree = new LinkedBinaryTree(node1);

中序遍历递归

上述代码中先序遍历的实现对用户不友好，而且增大了内存的开销，所以在中序遍历中改进如下

@Override
public void inOrderTraverse() {
    System.out.println("中序遍历");
    inOrderTraverse(this.root);
    System.out.println();
}
//	分装好遍历的函数，对用户及测试人员友好
private void inOrderTraverse(Node node) {
    if (node != null) {
        //  遍历左子树
        //	递归遍历左子树
        inOrderTraverse(node.leftChild);
		//	中根
        System.out.print(node.data + " ");

        //  遍历右子树
        inOrderTraverse(node.rightChild);
    }
}

中序遍历非递归(栈)

使用栈的先进先出特性可以实现非递归中序遍历

//  使用非递归的方式实现中序遍历
@Override
public void inOrderTraverseByStack() {
    System.out.println("非递归中序遍历");
    //	自己编写的栈，也可以用java中的Deqeue作为栈
    ArrayStack stack = new ArrayStack(7);
    //  遍历每一个结点，从根结点开始
    Node current = this.root;
    //  改变当前的结点，是的每个结点都作为根结点来遍历
    //  根结点不为空  栈不为空
    while (current != null || !stack.isEmpty()) {
        //  将所有的左子树存入栈
        while (current != null) {
            stack.push(current);
            current = current.leftChild;
        }

        if (!stack.isEmpty()) {
            //  通过这个弹出栈的操作，实现了回退功能
            current = (Node) stack.pop();
            System.out.print(current.data + " ");
            current = current.rightChild;
        }
    }
}

/**
 *  理解
 */
public void inOrderStack() {
    System.out.println("非递归中序遍历");
    ArrayStack stack = new ArrayStack(7);

    Node current = this.root;
    while (current != null || !stack.isEmpty()) {
        //  1、将某一个结点的所有不为空的左孩子入栈
        if (current != null) {
            stack.push(current);
            current = current.leftChild;
        } else {
            // 2、某一个结点所有的左孩子入栈成功，将最后一个入栈的左孩子弹出，再看看其右孩子，非空的话就重复第 1 步。
            current = (Node) stack.pop();
            System.out.print(current.data + " ");
            current = current.rightChild;
        }
    }
    System.out.println();
}

层序遍历(队列)

//  使用队列,先进先出
@Override
public void floorOrderTraverse() {
    System.out.println("层序遍历");
    if (this.root == null) {
        return;
    }

    ArrayQueue queue = new ArrayQueue(20);
    //  先将根结点放进去
    queue.add(this.root);
    //  队列不是空的，开始循环
    while (!queue.isEmpty()) {
        //  得到当前队列的长度(上一个状态结束时，队列的长度，实际上就是每一层的结点的个数)
        int len = queue.size();
        //  遍历这一层
        for (int i = 0; i < len; i++) {
            Node node = (Node) queue.poll();
            System.out.print(node.data + " ");
            /*
                 *   取出第 k层的第 i个结点，判断这个结点i有无子结点(实际上这些子结点就是第k+1层的结点),
                 *   如果!=null,则将这个k+1层的结点加入队列(等到第k层的结点出队列后才能轮到刚刚加入的这个第k+1层的结点)
                 */
            if (node.leftChild != null) {
                queue.add(node.leftChild);
            }
            if (node.rightChild != null) {
                queue.add(node.rightChild);
            }
        }
        System.out.println();
    }
}

层序遍历也就是广度优先遍历

案例

树的高度递归

如图二叉树:
								  1
							  /   \
							4		   2
							  \   /   \
							   5 3		 6
							   			     \
							   				    7
结点i的左子树记为:Li
结点i的右子树记为:Ri
结点i的(子)树的深度记为:Hi

1、
	H1 = H4 > H2? H4+1 : H2 + 1	即比较L1和R1的深度H4, H2,谁大选谁，再加一
2、
	H4 = H5 + 1
	H2 = H3 > H6? H3+1 : H6 + 1
3、
	H3 = 0 + 1		即	if(node==null) {return 0}; H3 没有左子树和右子树
	H6 = H7 + 1
4、
	H7 = 0 + 1

如果还有结点，递归即可

结点个数递归

如图二叉树:
1
/ \
 4 2
\ / \
 5 3 6
\
 7
实际上同 getHeight 原理, 都是递归

结点为 i 的(子)树的结点数目记为 ni

则:
n1 = n4 + n2 + 1
n4 = n5 + 1
n5 = 1
n2 = n3 + n6 + 1
n3 = 1
n6 = n7 + 1
n7 = 1
=> n1 = 7

---

串

串：字符串
eg: S = "Mawenshu cool!"  T = "hello world"
子串: 串的连续的一部分
空串: S = ''

串的操作

赋值
复制
清空
销毁
拼接
求长
取子串
定位
比较

哈希映射

概述

前面的系列的查找中， 如果序列无序，那么就遍历比对，如果序列有序， 就比较中间的那个， 二分搜索，前者时间复杂度 O(n)，后者 O(logn)。现在想要将时间复杂度压缩至接近 O(1)如何做到？

我们安装某种约定好的规则， 将某种东西放在固定的地方， 比如说一号货架放一支笔， 二号货架放一本书， 三号货架等等， 我们要找笔就直接从一号货架去取，要找书就直接从二号货架取， 而不用取查看比对每个货架， 因为我们事先知道什么货架上对应着什么物品，

hash 映射， 就是将数据按照某一映射规律， 存储在一个固定的地址， 比如 将 key 存储在 addr 上， 我们可以用一个数学表达式 addr = f(key)， 来映射我们所存放的地址。

比如我们存放 1、2、3、4、... 12 。十二个数， 按照某一个映射函数 (假设 f(key) = (key+3) mod 12), 这样的话 数据 1 存放在 地址 4， 数据 2 存放在 地址 5、... 、 数据 12 存放在地址 3.

我们可以用一个数组来存储这些数据， 数组的下标刚好对应相关的地址，例如：

a[0] = 9; a[1] = 10; a[2] =11; a[3] = 12; a[4] = 1; a[11] = 8; 注 ：f(8) = 11

上述 一个地址存放着一个数据， 但是往往有不可避免的差错发生， 比如说有一组数据 12,13,14, 15, 16, 17, 24, 36, 48,...共 12 个， 且有一个长度为 12 的 hash 表， 我们发现 f(12) = 3, f(24) = 3; f(36) = f(48) = 3; 这四个数想要存放的地址是一样的，这时便会发生冲突(碰撞), 我们只能减少碰撞， 并不能完全消除碰撞； 那么如何减少碰撞呢？

1、开放定址法_线性探测法

当发现地址 a 已经存储了数据的时候， 去 a+1 的地址看看， 依次累加， 直到有一个地址可以存放数据或者所有地址无法继续存储---->想其他的办法

如果空间用完了， 无地可存怎么办， 比如在 地址为 0 的地方已经存储了数据 a[0] = 12, 那么当存储 24 的时候， 我们可以将 12 和 24 串起来成一个链表或者一个数组(此时原来的 a 数组是一个二维数组)，然后 a[0] 存储的不在是 12，而是 12-24 这个链表的首地址(头指针) ， 当然这样一来 哈希表的时间复杂度就不为 O(1)了

0 1 2 3 4 5 <---地址

---

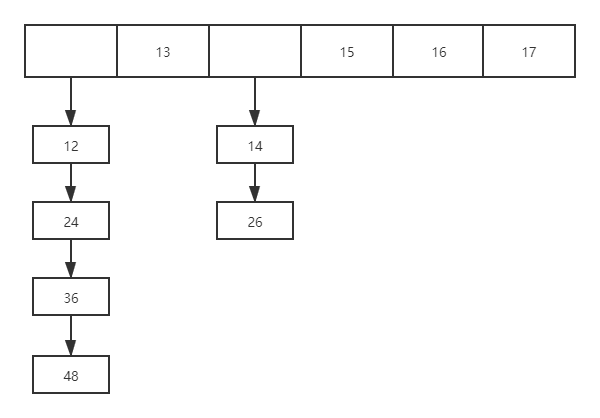
代码实现

public class HashTable {

  private Integer[] elements; *//* *用数组存储元素， 数组的索引模拟* *hash**地址*
    private Integer len; // 哈希表的长度

}



// 映射函数
private int getAddr(int n) {

  return Math.*abs*((n + 1) % this.len);
}

// 存储数据

private void insert(int n) {

  int addr = this.getAddr(n);

  while (this.elements[addr] != null) {

    addr = (addr + 1) % this.len; *//**处理冲突*

      if (addr == this.getAddr(n)) {

        System.*out*.println("数据已满, 更新数据存储");

      }

  }

  this.elements[addr] = n;

}

// 查找数据
private int search(int n) {

  int addr = this.getAddr(n);

  while (this.elements[addr] != n) {
    addr = (addr + 1) % this.len;

    if (addr == this.getAddr(n) || this.elements[addr] == null) {

      System.*out*.println("数据不存在");

      return -1;

    }

  }

  return addr;

}